青蛙跳台阶问题

1. 描述

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

2. 解题思路

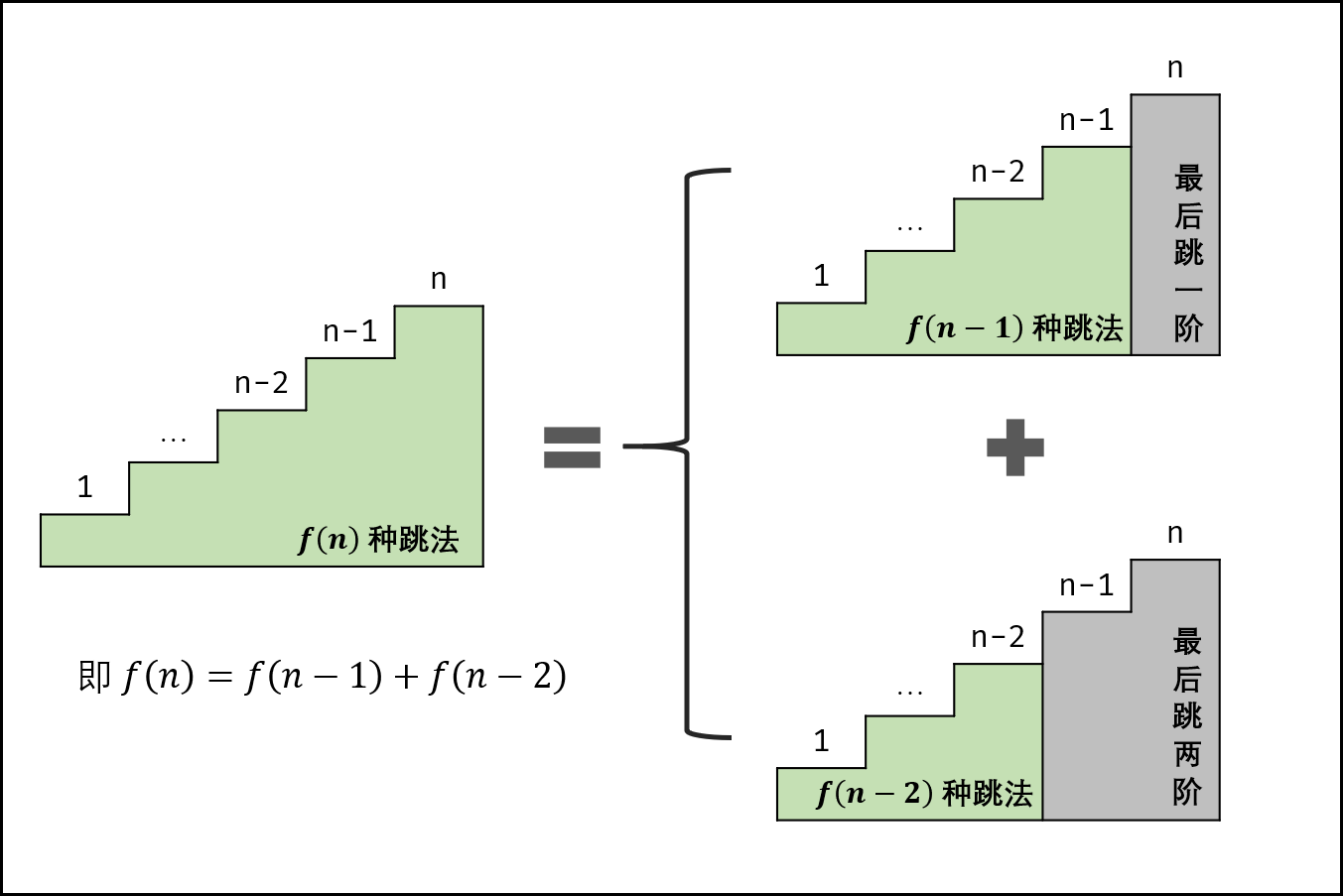
没看过过这个题，很难想出用递归的方法。青蛙到第n个台阶有两种可能性第一是从n-1台阶条一个台阶，第二种是从第n-2个台阶跳两个台阶。到n-1个台阶也有两种可能性...以此类推，一直到第零个与第一个台阶需要跳一个。

n	f(n)	备注
0	1
1	1
2	2	f(1) + f(0)
3	3	f(1) + f(2)
n	f(n)	f(n-1) + f(n-2)

3. 实现

（1）递归版

function numWays(n){
    if(n == 2 || n == 1 || n == 0) return n
    return numWays(n-1) + numWays(n-2)
}

（2）非递归版

var numWays = function (n) {
    var sum
    var a = 1
    var b = 1

    if (n < 2) return 1
    for (let i = 0; i < n - 1; i++) {
        sum = a + b
        [a,b] = [b,sum]
        // a = b
        // b = sum
    }

    return sum
};

来源： 剑指 Offer 10- II